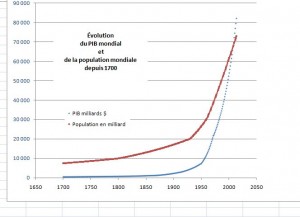
Voici un premier graphique réalisé par mes soins qui illustre la croissance du PIB et de la population mondiale.
Les lois exponentielles sont tout simplement impossibles au delà d’un certain temps dans un monde fini.
Tout le monde connait l’échiquier de Sissa (nombre de grain multiplié par deux qui au final font une valeur astronomique) ou l’équation du Nénuphar d’Albert Jacquard que je rappelle rapidement. On plante un nénuphar dans un grand lac. Ce nénuphar a la propriété héréditaire de donner un autre nénuphar chaque jour. Au bout de 30 jours il a recouvert la totalité du lac et la population meurt asphyxiée et privée de nourriture. Au bout de combien de temps recouvrait-il la moitié du Lac ? (réponse à la fin de l’article)
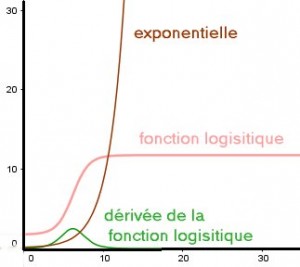
On connais trois type de fonction qui peuvent s’appliquer à notre monde.
- les exponentielles (pour un temps plus ou moins long)
- les courbes logistiques (ou sigmoïdes) qui rencontrent une limite d’une ressource renouvelable
- Les courbes en cloche d’une ressource finie
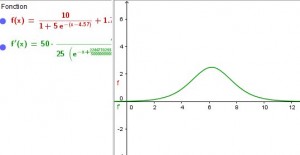
La loi logistique (ou sigmoïde) s’applique à une population qui exploite un milieu favorable et croit jusqu’à la limite de la capacité du milieu (généralement appelée capacité porteuse)
La courbe en cloche. La dérivé de la loi logistique s’applique à une ressource finie et elle est d’environ la moitié de la réserve totale. Elle décroit rapidement. On la retrouve dans le pic d’Hubbert.
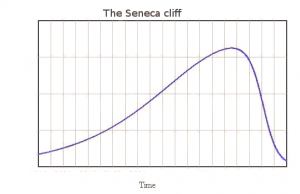
Si l’hypothèse d’Ugo Bardi est juste, l’utilisation d’une ressource finie rencontre une falaise de Sénèque, C’est à dire que l’utilisation de la ressource décroit brutalement.
Nous savons depuis les travaux de Gaël Giraud et Zeynep Kahraman que le PIB dépend de l’énergie disponible à 60 % environ et que l’accumulation du capital joue pour une faible part (10 %). Pourtant, c’est le capital que l’on rémunère.
Il semblerait que les découvertes scientifiques soient aussi soumises à une fonction logistique et donc que nous ne pouvons attendre notre salut de procédés nouveaux.
Les implications sont donc :
Il n’y aura plus de croissance. En théorie des jeux, les systèmes à somme nulle génèrent des gagnants et des perdants.
Les questions essentielles sont donc :
- Comment évaluer les limites du système ?
- Quelle est la taille de la population mondiale qui en résultera ?
- Quel sera le niveau de confort et de bien-être que nous pourrons avoir ?
- Allons nous subir un état stationnaire ou la descente rapide de la courbe en cloche à cause de l’utilisation massive de ressources finies ?
- la coopération l’emportera-t-elle sur le conflit entre les divers groupes humains ?
Pour aller plus loin
HANDY modélisation des limites et rôle des inégalités
Modèle Meadows actualisation de Turner sur l’effondrement
Pourquoi nous n’acceptons pas Piège et colère au moment des limites
La réponse était 29 jours c’est à dire à la toute fin car la surface occupée double tous les jours.